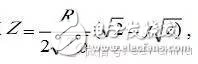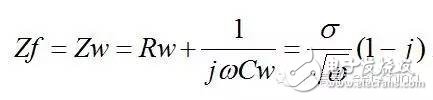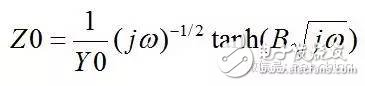|
电化学交流阻抗谱图
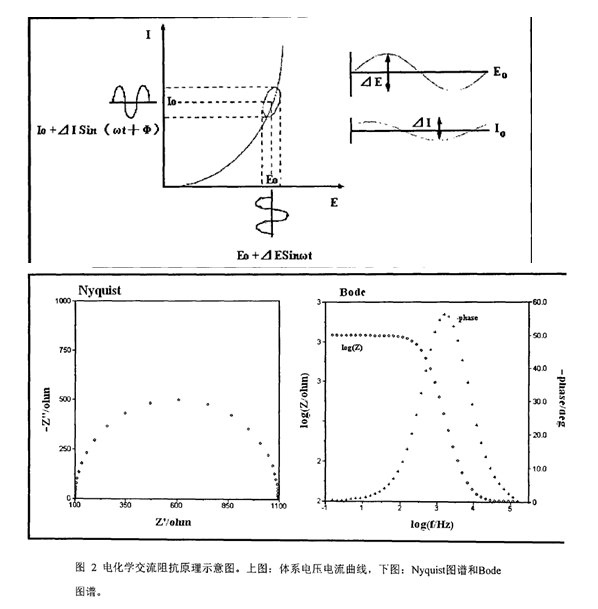
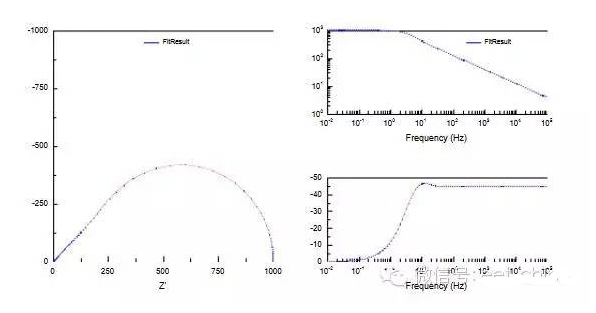
交流阻抗谱检测方法是给被测体系施加一个小振幅的单正弦波扰动,或者是不同频率正弦波的叠加,一般是正弦波形式的电压或者是电流,结果产生相应的电流或电压的响应信号。 如图2上图电流电压曲线所示,在体系直流电压E。的条件下外加正弦波电压Esin(ωt)(ω为角频率),那么在直流电流I0的基础上就会得到一个正弦波电流I=sin(ωt+Ф)。得到的电流响应值I受外加电压E控制。根据欧姆定律Z(ω)=E(ω)/I(ω)可计算出在某个频率下体系的阻抗值z。
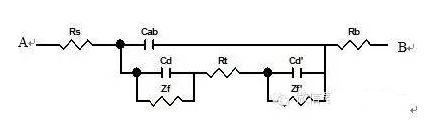
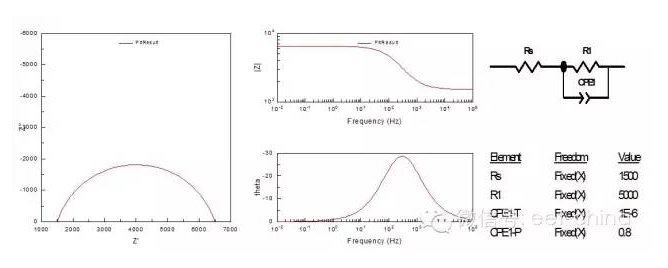
在电化学阻抗技术中,z被定义为一个复数,即Z(ω)=Zre(ω)+jZim(ω),Z2=Zre2+Zim2。其中实部 Zre=∣ Z∣cosθ,虚部Zim=∣Z∣Sinθ相位角θ=tan-1(Zim/Zre)。 以Zre对Zim作图,称为Nyquist图谱(如图2下图左图谱所示),可以清晰地给出实部和虚部的数值,并可进行体系定性分析。但它不能给出频率信息,所以通常要采用其它曲线来补充。 另外一种常用的表示方法是Bode图,即lgZ、相角对频率作图(如图2下图右图谱所示),图谱中同时表示了阻抗与频率、相移与频率的关系。 一般Nyquist图谱比较普遍,Nyquist图谱是由一个半圆部分和一个线性部分组成,半圆部分在高频区,对应的是电子转移限制过程,半圆越大,电阻就越大,后面直线部分在低频范围,对应的是扩散限制过程。 1、阻抗谱中的基本元件 交流阻抗谱的解析一般是通过等效电路来进行的,其中基本的元件包括:纯电阻R,纯电容C,阻抗值为1/jωC,纯电感L,其阻抗值为jωL。实际测量中,将某一频率为ω的微扰正弦波信号施加到电解池,这是可把双电层看成一个电容,把电极本身、溶液及电极反应所引起的阻力均视为电阻,则等效电路如图1所示。
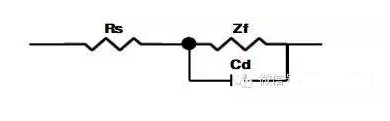
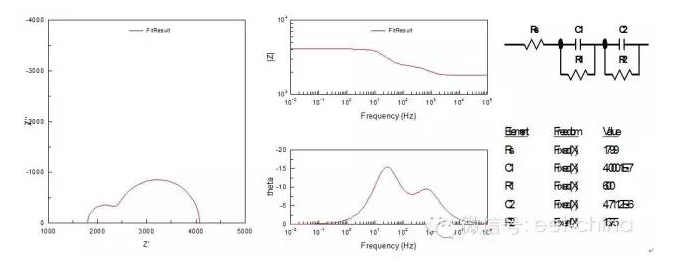
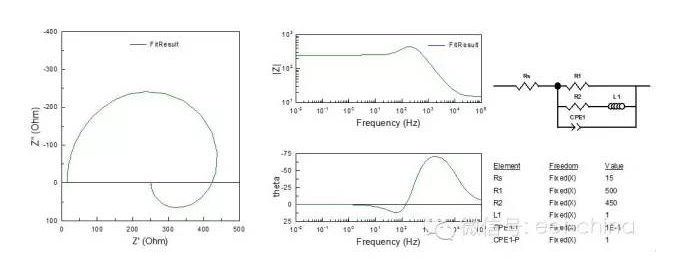
图1.用大面积惰性电极为辅助电极时电解池的等效电路 图中A、B分别表示电解池的研究电极和辅助电极两端,Ra、Rb分别表示电极材料本身的电阻,Cab表示研究电极与辅助电极之间的电容,Cd与Cd’表示研究电极和辅助电极的双电层电容,Zf与Zf’表示研究电极与辅助电极的交流阻抗。通常称为电解阻抗或法拉第阻抗,其数值决定于电极动力学参数及测量信号的频率,Rl表示辅助电极与工作电极之间的溶液电阻。一般将双电层电容Cd与法拉第阻抗的并联称为界面阻抗Z。 实际测量中,电极本身的内阻很小,且辅助电极与工作电极之间的距离较大,故电容Cab一般远远小于双电层电容Cd。如果辅助电极上不发生电化学反映,即Zf’特别大,又使辅助电极的面积远大于研究电极的面积(例如用大的铂黑电极),则Cd’很大,其容抗Xcd’比串联电路中的其他元件小得多,因此辅助电极的界面阻抗可忽略,于是图1可简化成图2,这也是比较常见的等效电路。
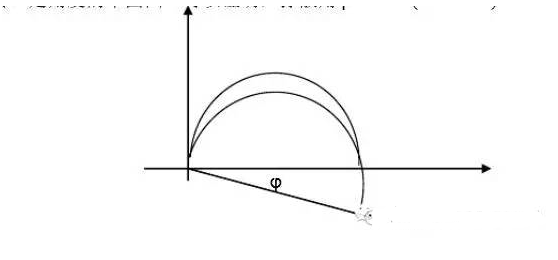
图2.用大面积惰性电极为辅助电极时电解池的简化电路 2、阻抗谱中的特殊元件 以上所讲的等效电路仅仅为基本电路,实际上,由于电极表面的弥散效应的存在,所测得的双电层电容不是一个常数,而是随交流信号的频率和幅值而发生改变的,一般来讲,弥散效应主要与电极表面电流分布有关,在腐蚀电位附近,电极表面上阴、阳极电流并存,当介质中存在缓蚀剂时,电极表面就会为缓蚀剂层所覆盖,此时,铁离子只能在局部区域穿透缓蚀剂层形成阳极电流,这样就导致电流分布极度不均匀,弥散效应系数较低。表现为容抗弧变“瘪”,如图3所示。另外电极表面的粗糙度也能影响弥散效应系数变化,一般电极表面越粗糙,弥散效应系数越低。 2.1、常相位角元件(ConstantPhaseAngleElement,CPE) 在表征弥散效应时,近来提出了一种新的电化学元件CPE,CPE的等效电路解析式为:
角为φ=--pπ/2,由于它的阻抗的数值是角频率ω的函数,而它的幅角与频率无关,故文献上把这种元件称为常相位角元件。 实际上,当p=1时,如果令T=C,则有Z=1/(jωC),此时CPE相当于一个纯电容,波特图上为一正半圆,相应电流的相位超过电位正好90度,当p=-1时,如果令T=1/L,则有Z=jωL,此时CPE相当于一个纯电感,波特图上为一反置的正半圆,相应电流的相位落后电位正好90度;当p=0时,如果令T=1/R,则Z=R,此时CPE完全是一个电阻。 一般当电极表面存在弥散效应时,CPE-P值总是在1~0.5之间,阻抗波特图表现为向下旋转一定角度的半圆图。
图3具有弥散效应的阻抗图 可以证明,弥散角φ=π/2*(1-CPE-P), 特别有意义的是,当CPE-P=0.5时,CPE可以用来取代有限扩散层的Warburg元件,Warburg元件是用来描述电荷通过扩散穿过某一阻挡层时的电极行为。在极低频率下,带电荷的离子可以扩散到很深的位置,甚至穿透扩散层,产生一个有限厚度的Warburg元件,如果扩散层足够厚或者足够致密,将导致即使在极限低的频率下,离子也无法穿透,从而形成无限厚度的Warburg元件,而CPE正好可以模拟无限厚度的Warburg元件的高频部分。当CPE-P=0.5时,
,其阻抗图为图3所示,一般在pH》13的碱溶液中,由于生成致密的钝化膜,阻碍了离子的扩散通道,因此可以观察到图4所示的波特图。
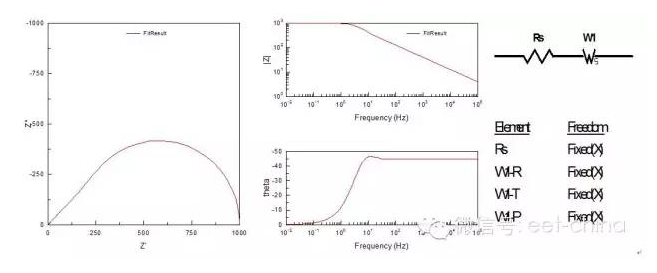
图4.当CPE-P为0.5时(左)及在Na2CO¬3溶液中的波特图 2.2、有限扩散层的Warburg元件-闭环模型 本元件主要用来解析一维扩散控制的电化学体系,其阻抗为,一般在解析过程中,设置P=0.5,并且Ws-T=L2/D,(其中L是有效扩散层厚度,D是微粒的一维扩散系数),计算表明,当ω-》0时,Z=R,当ω-》+∞,在
,与CPE-P=0.5时的阻抗表达式相同,阻抗图如图5。
图5.闭环的半无限的Warburg阻抗图 2.3、有限扩散层的Warburg元件-发散模型 本元件也是用来描述一维扩散控制的电化学体系,其阻抗为,其中ctnh为反正且函数,F(x)=Ln[(1+x)/(1-x)]。与闭环模型不同的是,其阻抗图的实部在低频时并不与实轴相交。而是向虚部方向发散。即在低频时,更像一个电容。典型的阻抗图如图6。
图6.发散的半无限的Warburg阻抗图 3、常用的等效电路图及其阻抗图谱 对阻抗的解析使一个十分复杂的过程,这不单是一个曲线拟合的问题,事实上,你可以选择多个等效电路来拟合同一个阻抗图,而且曲线吻合的相当好,但这就带来了另外一个问题,哪一个电路符合实际情况呢,这其实也是最关键的问题。他需要有相当丰富的电化学知识。需要对所研究体系有比较深刻的认识。而且在复杂的情况下,单纯依赖交流阻抗是难以解决问题的,需要辅助以极化曲线以及其它暂态试验方法。 由于阻抗测量基本是一个暂态测量,所以工作电极,辅助电极以及参比电极的鲁金毛细管的位置极有要求。例如鲁金毛细管距离参比电极的位置不同,在阻抗图的高频部分就会表现出很大的差异,距离远时,高频部分仅出现半个容抗弧,距离近时,高频弧变成一个封闭的弧;当毛细管紧挨着工作电极表面时,可能会出现感抗弧,这其中原因还不清楚。 为了有利于大家在今后的试验中对阻抗图有一个粗略的认识,下面简单将几种常见阻抗图谱介绍一下。 3.1、吸附型缓蚀剂体系 如果缓蚀剂不参与电极反应,不产生吸附络合物等中间产物,则它的阻抗图仅有一个时间常数,表现为变形的单容抗弧,这是由于缓蚀剂在表面的吸附会使弥散效应增大,同时也使双电层电容值下降,其阻抗图及其等效电路如图7。
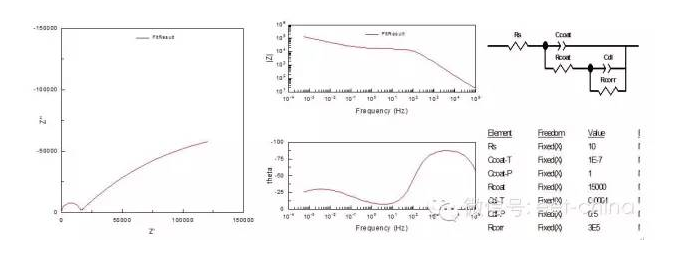
图7.具有一个时间常数的单容抗弧阻抗图 3.2、涂层下的金属电极阻抗图 涂装金属电极存在两个容性时间常数,一个时涂层本身的电容,另外一个是金属表面的双电层电容,阻抗图上具有双容抗弧,如图8所示。
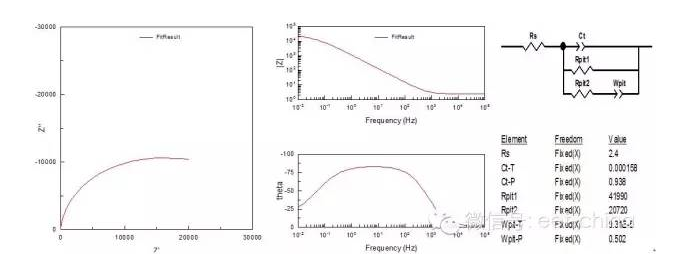
图8.具有两个时间常数的涂层金属阻抗图 等效电路中的Ccoat为涂层本身的电容,Rcoat为涂层电阻,Cdl为涂层下的双电层电容,当溶液通过涂层渗透到金属表面时,还会有电化学反应发生,Rcorr为电极反应的阻抗。 3.3、局部腐蚀的电极阻抗图 当金属表面存在局部腐蚀(点腐蚀),点蚀可描述为电阻与电容的串联电路,其中电阻Rpit为蚀点内溶液电阻,一般Rpit=1~100Ω之间。而是实际体系测得的阻抗应为电极表面钝化面积与活化面积(即点蚀坑)的界面阻抗的并联耦合。但因钝化面积的阻抗远远高于活化免得阻抗,因而实际上阻抗频谱图反映了电极表面活化面积上的阻抗,即两个时间常数叠合在一起,表现为一个加宽的容抗弧。其阻抗图谱与等效电路如图9所示。
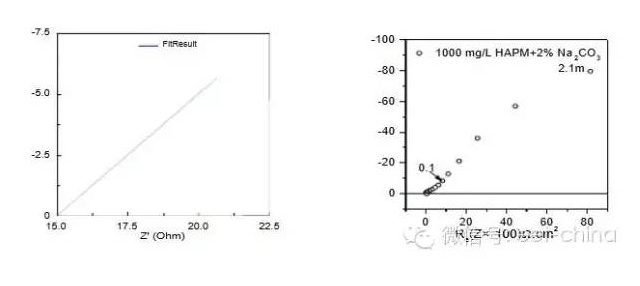
图9.表面存在局部腐蚀时阻抗图 3.4、半无限扩散层厚度的电极阻抗图 所谓半无限扩散过程,是指溶液中的扩散区域,即在定态下扩散粒子的浓度梯度为一定数值的区域,扩散层厚度为无穷大,不过一般如果扩散层厚度大于数厘米后,即可认为满足这一条件。此时法拉第阻抗就等于半无限扩散控制的浓差极化阻抗Zw与电极反应阻抗Zf的串联,其阻抗
,电极反应完全受扩散步骤控制,外加的交流信号只会引起表面反应粒子浓度的波动,且电极表面反应粒子的浓度波动相位角正好比交流电流落后45度,阻抗图为45度角的倾斜直线,如图10所示。如果法拉第阻抗中有Warburg阻抗,则Rp无穷大,但在腐蚀电位下,由于总的法拉第阻抗是阳极反应阻抗与阴极反应阻抗的并联,一般仅有阴极反应有Zw,故此时总的Rp应为阳极反应的Rp1值,Zf仍为有限值。 当电极表面存在较厚且致密的钝化膜时,由于膜电阻很大,离子的迁移过程受到极大的抑制,所以在低频部分其阻抗谱也表现为一条45度倾角的斜线。
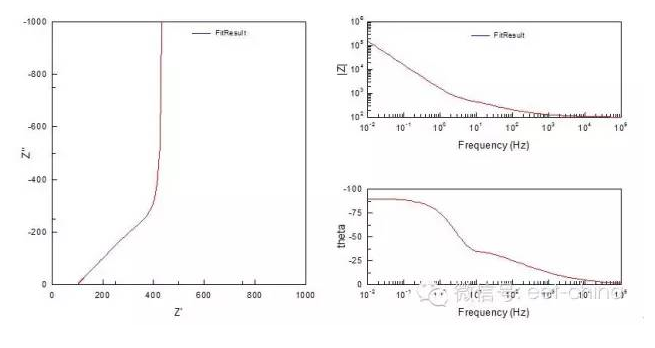
图10.表面存在致密的钝化膜时的阻抗图 3.5、有限扩散层厚度的电极阻抗图 当扩散层厚度有限时,即在距电极表面l处,扩散粒子的浓度为一不随时间变化的定值,则有
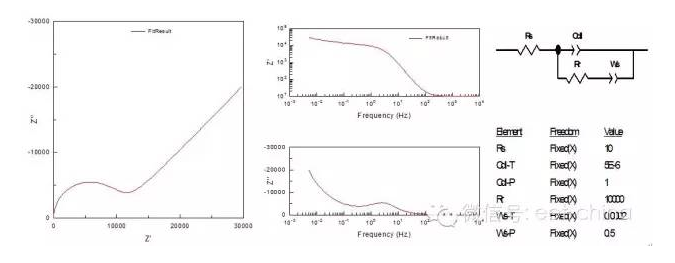
,在低频是完全由浓差扩散控制,但在高频使它相当于一个RC串联电路,见2.2节。实际测量中,当电极表面的存在扩散层控制时,在较低频率下,离子的迁移过程可以通过延长时间来扩散到金属表面,发生电化学反应,因此波特图表现为一闭合的圆弧,可以用有限扩散层厚度的Warburg阻抗来模拟,如图11所示。
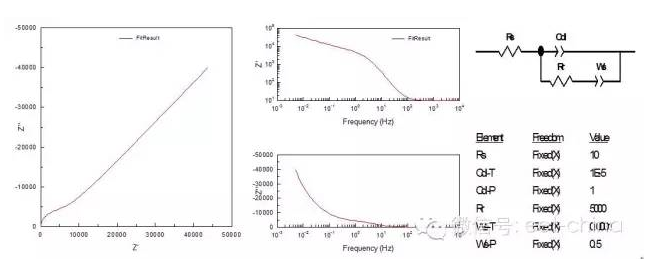
图11.表面存在非致密的钝化膜时的阻抗图 3.6、同时受电化学和浓差极化控制 在混合控制下,交流信号通过电极时,除了浓差极化外还将出现电化学极化,这时电极的法拉第阻抗比较复杂,在高频部分为双电层的容抗弧,而在低频部分,扩散控制将超过电化学控制,出现Warburg阻抗,其等效电路及阻抗图如图12所示。
图12.同时受扩散和电化学控制的阻抗图 3.7、具有双容抗弧的电化学阻抗 另外如果法拉第电流If不仅与极化电位E有关,而且与某一表面状态变量X相关,则由于X对电位的响应会引起弛豫现象,从而出现除双电层电容以外的第二个时间常数,不过这第二个时间常数即可能是容性的也可能是感性的,这取决于B值,当B》0时,低频出现感抗弧,当B《0时,则在低频出现第二个容抗弧。某些吸附型物质在电极表面成膜后,这层吸附层覆盖于紧密双电层之上,且其本身就具有一定的容性阻抗Cf,它与电极表面的双电层串联在一起组成具有两个时间常数的阻抗谱,其阻抗图如图13所示。
图13.具有两个时间常数的阻抗图 3.8、低频出现感抗弧的电化学体系 前面说过,当法拉第电流不仅与电极电位有关,而且受电极表面状态变量X影响,而这个状态变量本
弧。 当电极反应出现中间产物时,这种中间产物吸附与金属电极表面产生表面吸附络合物,该表面络合物产生于电极反应的第一步,而消耗于第二步反应,而一般情况下,吸附过程的弛豫时间常数要比电双层电容Cdl与Rt组成的充放电过程的弛豫时间常数RtCdl大的多,因此在阻抗图的低频部分会出现感抗弧。如图14所示。
图14.低频出现感抗弧的阻抗图
电容,整个EIS出现两个容抗弧,如图13所示。 混合电位下的阻抗谱特征 上面所述的阻抗谱均是在自然电位下测量的,而电极反应在自然电位下同时具有阴阳极两个反应,所以阻抗谱所反映的是两个电极反应的频谱特征,即文献所述的混合电位下的阻抗谱,当没有状态变量时,EIS仍只有一个时间常数,当有一个状态变量影响电极反应速度时,阻抗谱会出现两个时间常数。不过在某些情况下,需要研究单一阳极反应特征,就必须将研究电极的电位极化(弱极化区)到不同的阳极电位下进行阻抗测量,以抑制阴极反应,这就是所谓的直流偏压下的阻抗测试,这一点在研究钝化膜的临界破裂电位下的阻抗特征尤为重要,它能提供点蚀诱发期的重要特征,另外在研究缓蚀剂的阳极脱附行为时也十分重要。 交流阻抗的不足之处 前面指出,对于同一组抗谱,可以找到不止一个电路能满足它的解析,而对于同一个电路,当电路中的元件参数不同时,可以得到完全不同类型的阻抗谱,因此依靠等效电路来推测电极过程的动力学机构是一个不可靠的方法。 (责任编辑:admin) |