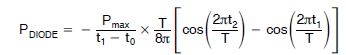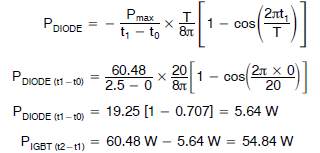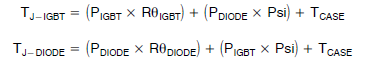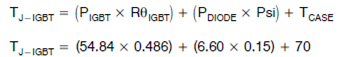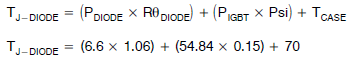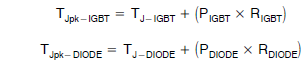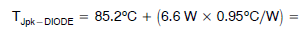|
与大多数功率半导体相比,IGBT 通常需要更复杂的一组计算来确定芯片温度。这是因为大多数 IGBT 都采用一体式封装,同一封装中同时包含 IGBT 和二极管芯片。为了知道每个芯片的温度,有必要知道每个芯片的功耗、频率、θ 和交互作用系数。还需要知道每个器件的 θ 及其交互作用的 psi 值。 本应用笔记将简单说明如何测量功耗并计算二极管和 IGBT 芯片的温升。 损耗组成部分 根据电路拓扑和工作条件,两个芯片之间的功率损耗可能会有很大差异。IGBT 的损耗可以分解为导通损耗和开关(开通和关断)损耗,而二极管损耗包括导通和关断损耗。准确测量这些损耗通常需要使用示波器,通过电压和电流探针监视器件运行期间的波形。测量能量需要用到数学函数。确定一个开关周期的总能量后,将其除以开关周期时间便可得到功耗。
图 1. TO−247 封装,显示了 IGBT 芯片(左)和二极管芯片(右) IGBT开通
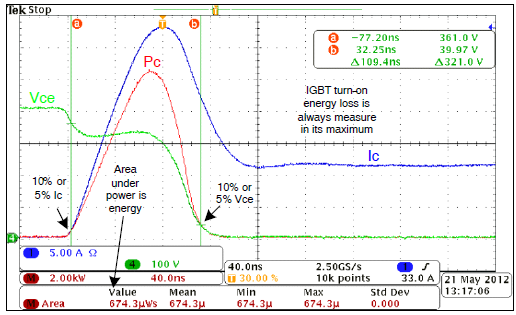
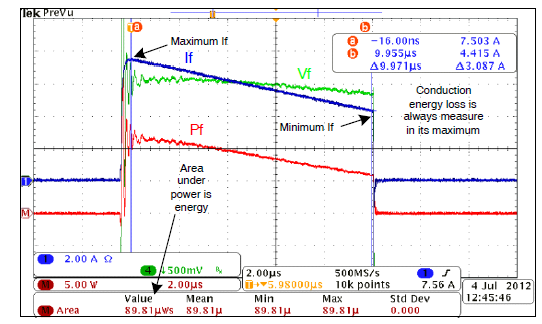
图 2. IGBT 开通损耗波形 将开通波形的电压和电流相乘,即可计算出该周期的功率。功率波形的积分显示在屏幕底部。这就得出了 IGBT 开通损耗的能量。 功率测量开始和结束的时间点可以任意选择,但是一旦选定了一组标准,测量就应始终遵循这些标准。IGBT导通损耗
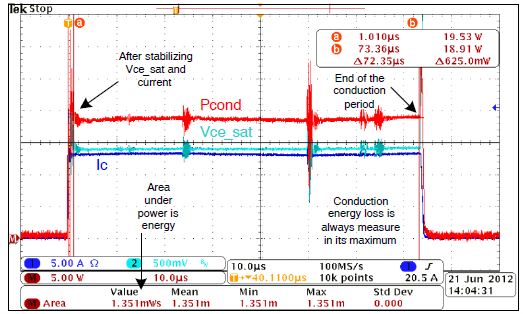
图 3. IGBT 传导损耗波形 导通损耗发生在开通损耗区和关断损耗区之间。同样应使用积分,因为该周期内的功率并不是恒定的。 IGBT关断
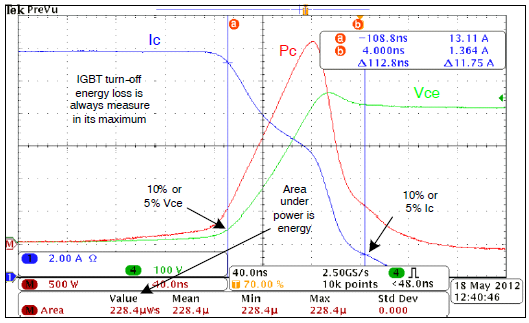
图 4. IGBT 关断损耗波形 开通、导通和关断损耗构成了 IGBT 芯片损耗的总和。关断状态损耗可以忽略不计,不需要计算。为了计算 IGBT 的总功率损耗,须将这三个能量之和乘以开关频率。
IGBT 损耗必须使用阻性负载或在负载消耗功率的部分周期内进行测量。这样可消除二极管导通。
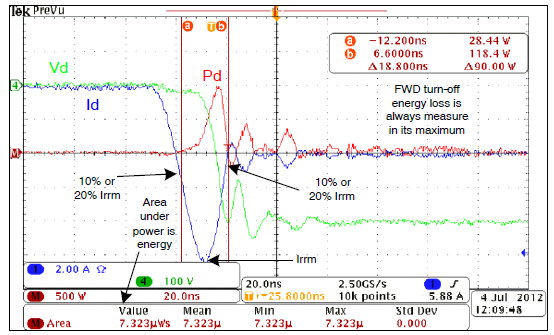
图 5. 二极管导通损耗波形 FWD反向恢复
图 6. 二极管反向恢复波形 图 5 和图 6 显示了二极管在整流器或电抗模式下工作期间的电流和电压波形。二极管损耗的计算类似于 IGBT 损耗。
IGBT 和二极管功耗计算 测量完这五个损耗分量后,需要将它们与测量条件相关联,以便计算每个芯片的总功耗。
图 7. 感性负载波形 图 7 显示了感性负载(如电机)的典型电压和电流波形。 从 t0 到 t1,电流为电抗性,二极管传导电流。 从 t1 到 t2,电流为阻性,IGBT 传导电流。 这些时间段的功耗具有重要价值。基于单个脉冲计算每个时间段的平均功耗非常复杂,但我们可以合理的精度进行估算。为此,我们需要计算该时间段的平均功耗。 在这种情况下,有必要计算平均(或加热)当量。对于电压和电流值,它是均方根值;对于功率,它是平均值。平均功耗
此公式计算的是正弦波每个四分之一部分的功率,因此要进行校正,我们需要在分母中添加一个因子 4。只要电压过零点在 0° 和 90°之间(对于感性负载必定如此),这就是有效的,故公式变为:
二极管 二极管在 t0 到 t1 期间传导电流。利用电压过零点的波形可得出二极管的峰值功耗。知道此功耗值后,我们可以使用 t0 到 t1 期间的平均功耗公式来求得二极管的平均功耗。 此时间段的示例计算如下所示。 PDIODEpk = 50 W(在电压过零点) T = 20 ms(50 Hz 正弦波) t0 =0 t1 = 2.5 ms 2 W 功率出现在进入周期后的 2.5 ms 时。要计算正弦波峰值处的等效功率,我们需要比较这两点的幅度。峰值幅度出现在 90° 或 π/2 弧度处,相当于幅度 1。2.5 ms 处的幅度为 sin(π × 2.5 ms/10 ms) 或 0.707,因此正弦波峰值处的功率为:
IGBT 对于正电压半周期,IGBT 在 t1 到 t2 期间传导电流。IGBT 的平均功耗计算与二极管功耗的计算方法类似。其示例计算如下所示。 PIGBTpk = 95W T = 20 ms(50 Hz 正弦波) T1 = 2.5 ms T2 = 10 ms (T/2) 对于 IGBT 分析,我们将计算完整半正弦波期间 (t0 – t2) 的 IGBT 功耗,然后计算二极管导通期间 (t0 – t1) 的 IGBT 功耗,再从前一功耗中减去后一功耗。
由于 t2 = T/2,故公式变为
芯片温度计算 一旦计算出两个芯片的功耗值,就可以使用数据表中的曲线计算芯片温度。两个芯片的温度一般不相同。每个芯片有一个 θ,并有一个交互作用系数 Psi。θ 是从芯片到封装外壳或引线的热阻,它有不同的名称,例如 RΘJC 是结至外壳热阻。Psi 是一个常数,表示芯片中未被计算的热效应。它基于芯片之间的距离。 通常,对于 IGBT 使用的大多数 TO-247 和 TO-220 封装,0.15°C/W 是一个合理的估计值。
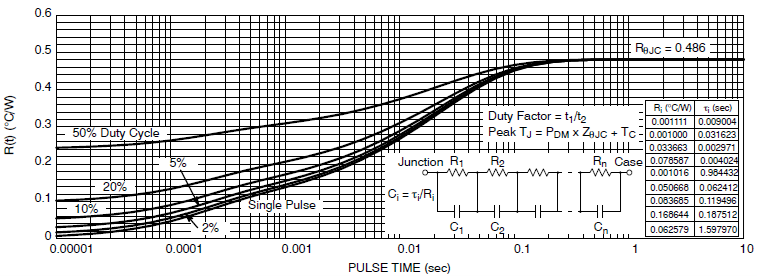
图 8. IGBT 热曲线
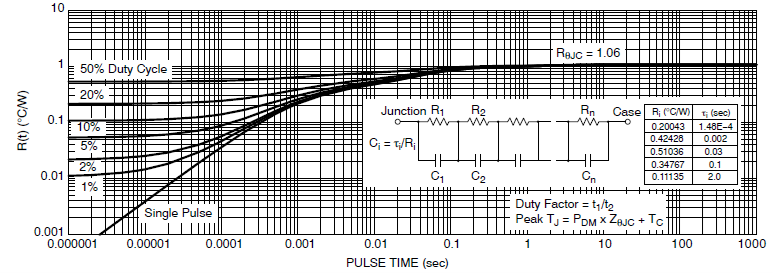
图 9. 二极管热曲线 图 8 和图 9 显示了典型封装中 IGBT 和二极管的热响应曲线。曲线上给出了直流值。对于 IGBT,它是 0.486°C/W;对于二极管,它是 1.06°C/W。 为了计算给定功率水平对应的稳态温度,只需要功耗值、直流 θ 和外壳温度。计算如下:
示例: TC = 70°C RΘJC-IGBT = 0.486°C/W RΘJCdiode = 1.06°C/W PD-IGBT = 54.84 W PD-DIODE = 6.60 W 交互作用系数 Psi = 0.15°C/W IGBT 的稳态结温为:
TJ-IGBT = 97.6°C(平均结温) 二极管的稳态结温为:
TJ-DIODE = 85.2°C(平均结温) 为了计算峰值结温,我们可以将脉冲值增加到稳态(或平均)温度中。此计算需要上述计算得出的结温,并加上瞬时温度变化。 唯一需要的新常数是 IGBT 或二极管对于所需脉冲宽度的脉冲值。在 50 Hz 的线频率下,半周期的时间为 10 ms。根据图 8,对于 10 ms 脉冲和 50% 占空比,RIGBT 值为 0.375°C/W;根据图 9,相同条件下的 RDIODE 值为 0.95°C/W。 基本公式如下:
因此,对于上述条件,峰值结温为:
= 120°C(峰值结温)
= 91°C(峰值结温) 总结 仅使用 θ 值无法计算多芯片封装中的结温。利用从数字示波器获得的波形和数学公式,可以计算每个器件的功耗。给定 IGBT 的功耗、θ 和 psi,便可计算平均和峰值结温值。 审核编辑:陈陈 (责任编辑:admin) |




 需要了解的是,损耗以半正弦波变化。需要考虑从峰值到过零的变化,以得出器件的平均功耗。
需要了解的是,损耗以半正弦波变化。需要考虑从峰值到过零的变化,以得出器件的平均功耗。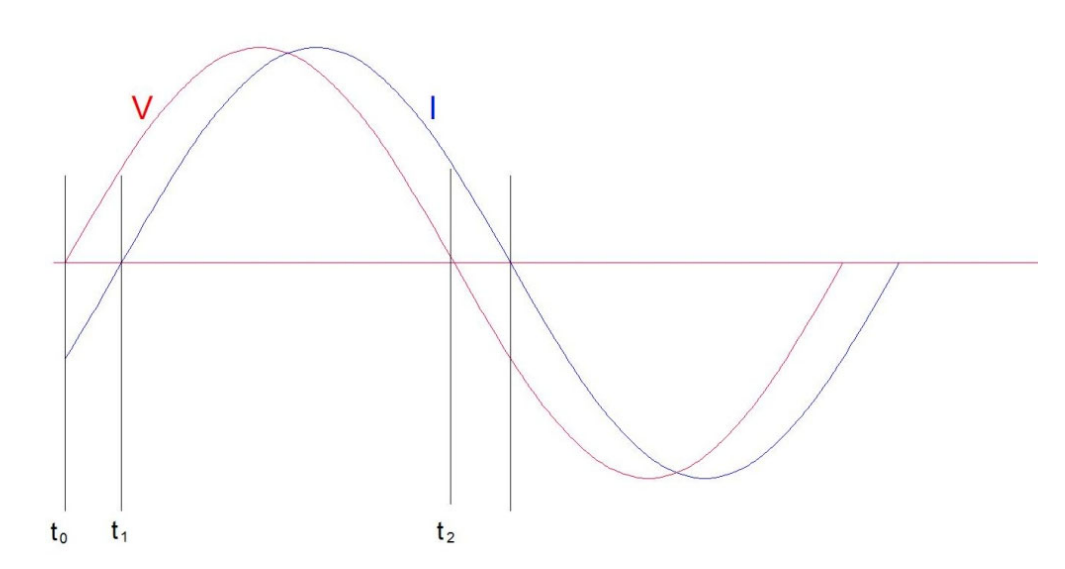
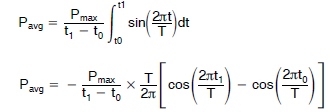
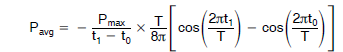
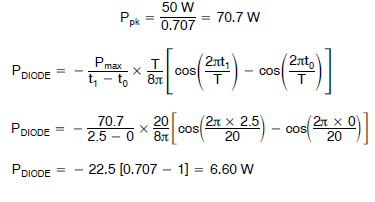
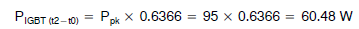 然后计算二极管导通期间的功耗
然后计算二极管导通期间的功耗