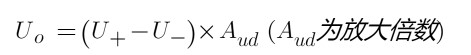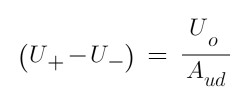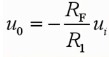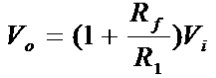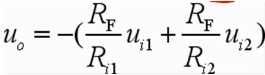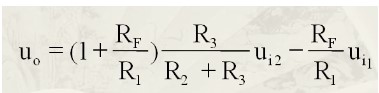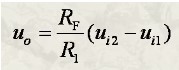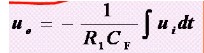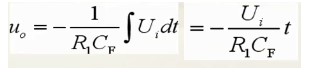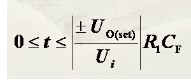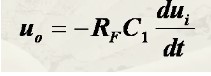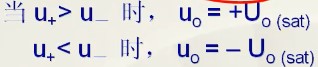|
一、集成运放器特点
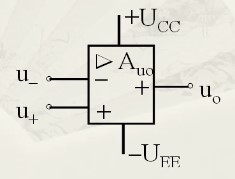
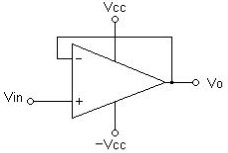
优点 高增益(可以配置较高的放大倍数) 输入阻抗高(对输入信号影响小) 输出阻抗低(对后级影响小) 共模抑制比较高,抗干扰能力强 1.1、当工作在线性区 运放器的放大倍数是一个很大的值,工作区指的是这个放大倍数有效的区域,因为一个运放器不可能无限放大(受限于供电电压和自身组成的元器件特性),所以放大后的输出电压有一定的范围,所以不可能超过这个范围,工作在这个范围内,放大倍数有效的区域叫做线性区,而输出电压触及到最大范围(此时放大倍数已失效,无论输入输出相差多大,电压维持在最大值),叫做非线性区。 两个重要特点 虚短(理想运放两端输入电压近似相等,即U+ = U-,故有虚短(不是绝对的短路,所以有点虚)的意思) 我们知道运放输出有如下公式,
转换得到如下公式,由于放大倍数很大,右边接近为0,所以得到U+ = U-的结论,即为我们所说的虚短。
一种个人理解,虽然公式是这样算,我们也可以一种感性的理解,由于运放的放大倍数很大,要想处于非线性区(上面解释线性区的时候说明了条件),则要求运放两端输入电压压差不能相差太大,所以就能得到U+约等于 U-,也就是虚短了。 虚断(理想运放的输入电流近似等于0,即 I+ = I- = 0) 由于运放的输入阻抗非常非常大,输入电压除以输入阻抗则接近0,所以运放器的两端的输入电流为0,就像断开一样,所以叫做虚断。 1.2、当工作在非线性区 此时输出只有两种可能:正最大、负最大。 其实可以当做比较器(一般来说单纯做比较器,成本会低些),更常见的是不提供负电压,则此时的情形是当U+> U-时,输出最大电压(主要有运放的供电电压决定),当U+< U-,输出0,这两个一高一低的状态,可以当做逻辑状态的1和0。
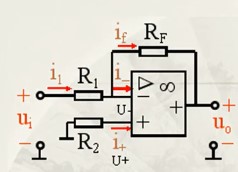
此时,仍满足虚断,但不满足虚短(看看线性区与非线性区的说明即可)。 二、集成运放器的应用 2.1、反相比例运算 ---- 输出与输入相位相反(即方向相反,负变正,正变负),大小成比例(放大或缩小) 反相比例运算的原理图如下,
得到输出与输入的关系如下(推导过程略):其中负号体现了反相这一特性。
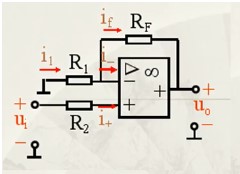
R1和Rf根据比例选取,R2一般是近似R1和Rf的并联值,能够增加电路的抗干扰能力。 注意: 工作在线性区,公式才有效。 应用:很多设备(单片机等)都只能检测到正压,如果要检测负压,可以先通过该方法将负压转换成正压,然后检测。 2.2、同相比例运算 电路原理图如下:
得到输出与输入的关系如下(推导过程见-- 百度百科:同相比例运算电路):
R1和Rf根据比例选取,R2一般是近似R1和Rf的并联值,能够增加电路的抗干扰能力。 注意: 工作在线性区,公式才有效。 电压跟随器 此外,同相比例运算有一个比较常用的形式:跟随器。(详细分析:电压跟随器的原理)
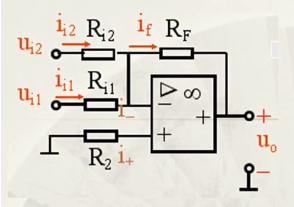
这种电路相当于同相放大一倍,那这样的电路存在的意义是什么? 存在即合理,电压跟随器常用作中间级,以 “隔离”前后级之间的影响 ,此时也称之为缓冲级。基本原理还是利用它的输入阻抗高(对输入信号影响小)和输出阻抗低(输出电压不易被输出端的负载影响)之特点,在电路中起阻抗匹配的作用。 2.3、反相加法运算 电路如下:
公式如下:
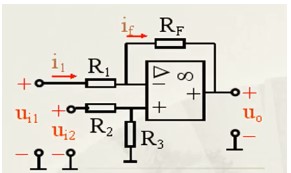
Ri1、Ri2和Rf根据比例选取,R2一般是近似Ri1、Ri2和Rf的并联值,能够增加电路的抗干扰能力。 注意: 工作在线性区,公式才有效。 2.4、减法运算
得到如下公式:
当R1=R2, R3=Rf时,得到如下公式:
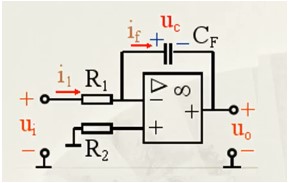
2.5、积分运算电路 电路如下:
得到输出的公式:(由虚短虚断和电容电流计算公式推导)
当输入信号为直流时,可以得到
其中,t是有限范围的,不然Uo就会是无穷大(最大能达到运放的供电电压,或正或负),t大过这个范围,则保持最大值,范围如下:
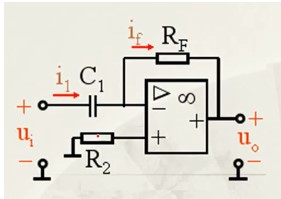
2.6、微分运算电路
输出公式如下:
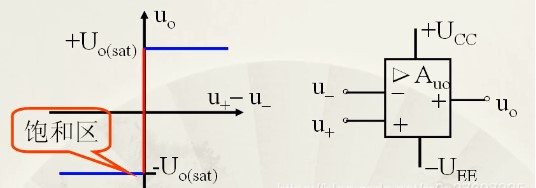
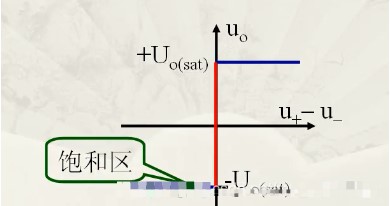
2.7、电压比较器 前面的电路,运放都是工作在线性区,而电压比较器就是工作在非线性区的一种情况。 构成电压比较器的电路的条件很简单:没有负反馈回路。 输出只有两种结果,如下:(当然,如果运放的负电压输入端接地,即接入为0V时,下面的-Uo(sat)为0,这也是一种比较常见的形式,毕竟提供负电压还是有些麻烦的)
输出的结果有输入两端电压决定,如下:
|