|
引自:《生产系统建模与仿真》(作者:朱海平)
「 1. 概述 」 在传统的车间计划安排中,计划方案的制定一般是由相关工作人员依靠经验进行安排,缺乏对整体计划安排的考虑和科学的定量分析。随着计算和运筹学的发展,出现了对各种类型的车间引入数学模型通过智能优化方法进行求解的方法。而简单抽象和忽略细节因素的数学模型往往不能对复杂车间进行准确的描述,对复杂车间投产计划优化效果甚微。结合生产系统仿真的优化技术与传统优化技术相比,其最大的优点是能够对存在物流、人力资源调度和随机因素的复杂车间进行准确描述,对各种生产排程方案进行准确且更贴近现实的比较、评价。生产系统仿真软件中,与算法相结合的生产计划仿真优化一般流程如下: (1)创建仿真模型。 (2)定义优化目标 :生产系统仿真优化目标可以涉及车间各个方面,如计划调度、物流效率优化、设施布局优化、资源调度优化等。以生产计划的优化为例,生产计划的性能指标可以分为最大能力指标、成本指标、客户满意度指标三类。涉及到生产效率与周期的指标一般可归为最大能力指标,涉及库存、利润、费用等内容的指标一般可归为成本指标,涉及到生产延迟、交货期等内容的指标一般可归为客户满意度指标。常用的指标包括最大完工时间、交货期满意度等。 (3)定义所选用的算法框架 :常用的算法有遗传算法、粒子群算法、禁忌搜索算法、模拟退火算法等。 (4)定义输入参数以及编码形式 :基于所采用的智能优化算法,将生产系统仿真模型中的参数,转化为智能优化方法的编码形式,编码形式包含了对所优化问题约束的体现,需要结合具体问题考虑采用不同编码方式。例如,对于流水车间调度问题一般采用正整数编码,对于柔性作业车间调度问题,一般采用MSOS两段式整数编码的方式。 (5)定义仿真试验初始化方法 :该方法在每次试验的每次观察仿真前自动执行,主要是对优化方法输出编码的解码过程。例如,对于流水车间调度问题,将正整数编码解码为投产的顺序,作为仿真模型的输入参数。 (6)定义算法的参数 :针对所选择的优化算法,初始化参数,以遗传算法为例,其参数包括种群数、优化代数、交叉算子、变异算子以及交叉变异概率等。 (7)定义仿真结束前方法 :该方法在每次试验的每次观察仿真结束前自动执行,主要作用是根据仿真结果来计算算法的优化评价结果,例如计算遗传算法中适应度函数值。 (8)仿真优化的自动运行。 (9)优化结果保存、输出与分析。 「 2. 生产计划单目标仿真优化 」 图1是一个并行流水车间的案例,“入口”处产生5类工件A、B、C、D、E,均需经过3到工序的加工。工序1可以在M001或M002上进行加工,工序2可以在M003或M004上进行加工,工序3可以在M005或M006上进行加工,加工完毕成品进入“出口”。相关基础数据如下: (1)A、B、C、D、E各投入5个,共25个,在0时刻同时投产; (2)5类工件在每台设备上加工的时间均不相同,加工时间如表1所示。
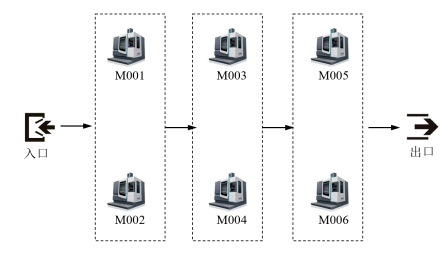 图1 生产计划单目标优化模型示例 表1 产品加工时间表 产品 工序1 工序2 工序3 M001 M002 M003 M004 M005 M006 A 5:0 15:0 8:0 17:0 35:0 12:0 B 18:0 28:0 12:0 8:0 15:0 15:0 C 11:0 35:0 16:0 36:0 6:0 21:0 D 8:0 22:0 25:0 46:0 7:0 36:0 E 20:0 11:0 38:0 38:0 13:0 16:0
不同的产品投产顺序,产品总完工时间不同,25个产品投产顺序的组合数为25!个,无法通过仿真试验设计得到最佳的批次投产顺序,下面通过智能优化算法结合仿真进行优化。
(1)创建仿真优化对象的仿真模型。
(2)优化目标:最小化最大完工时间。
(3)定义算法框架:选择遗传算法框架,其流程如图2所示。
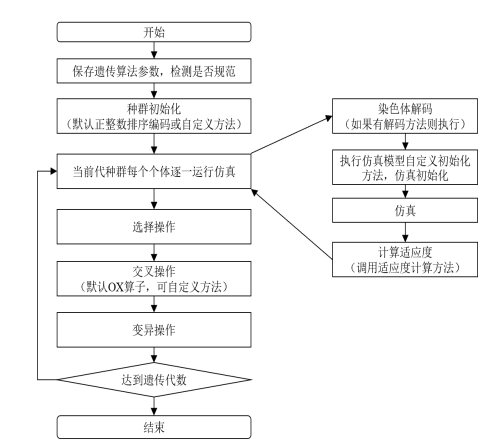 图2 基于遗传算法的仿真优化流程图
(4)定义输入参数以及编码形式:输入参数为25个产品的投产顺序,采用正整数编码的方式对染色体进行编码。
(5)定义解码方法:对染色体进行解码,编码1~5位代表A,编码6~10位代表B,编码11~15位代表C,编码16~20位代表D,编码21~25位代表E,染色体长度为25。解码后的顺序作为新的投产顺序输入仿真模型。
(6)定义算法的参数 :种群大小设置为100,进化代数设置为100,交叉变异概率分别取0.8和0.1。交叉算子采用部分映射交叉法(Partial Mapped Crossover, PMX)的方式。PMX的例子如图3所示,首先选取父代基因的起止位置,交换这两组基因;其次,进行冲突检测,子代冲突部分,经过映射关系变换为正常的子代染色体。变异算子采用互换变异,即在序列中随机选择两个基因,交换其在染色体上的位置后形成新的后代个体。
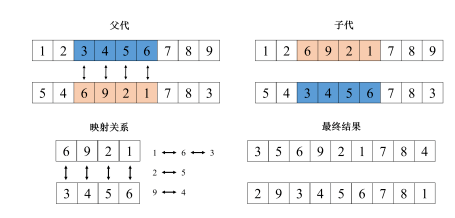 图3 PMX交叉算子 (7)定义适应度计算方法:通过仿真模型运行结果,获取仿真完工时间,作为遗传算法的适应度值。 (8)仿真优化自动运行。 (9)优化结果 :最优生产顺序为AECDCAAEBDBDECCEDCBEABABD。仿真初始结果为14天22时,优化后结果为12时7分,适应度收敛曲线如图4所示。
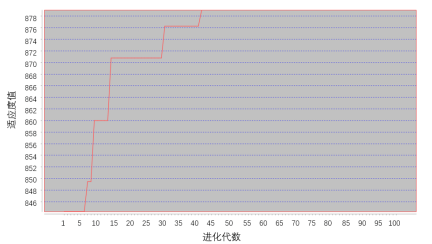 图4 适应度收敛曲线 「 3. 生产计划多目标仿真优化 」 下面通过一个复杂车间生产计划优化实例来介绍多目标仿真优化方法。图5所示为某焊接车间仿真模型。
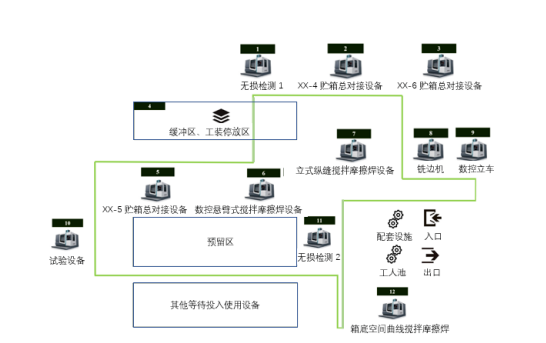 图5 焊接车间仿真优化模型实例 (1)车间布局如图5所示,面积约1.6万m2,生产运载火箭贮箱等大型复杂结构零件,车间在使用的设备或区域共12个,包括无损检测设备2台、XX-4/5/6总对接设备各1台、缓冲区和工装停放区域、数控悬臂式搅拌摩擦焊设备1台、立式纵缝搅拌摩擦焊设备1台、铣边机1台、数控立车1台、试验区包含试验设备1台、箱底空间曲线搅拌摩擦焊设备1台。 (2)车间生产XX-4、XX-5和XX-6三类贮箱产品,产品的生产工艺大致相同,若干壁板、瓜瓣、顶盖和型材框加工成筒段、短壳和单底,再由若干筒段、短壳和单底经过总对接焊接成最后的产品贮箱。产品BOM见图6,工艺流程见图7。
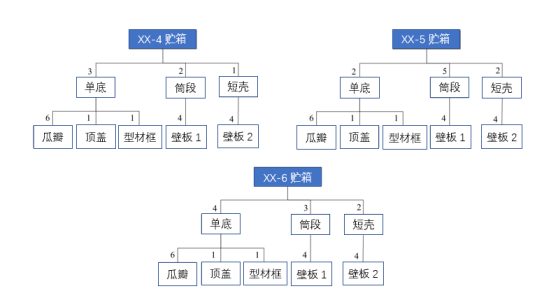 图6 产品BOM
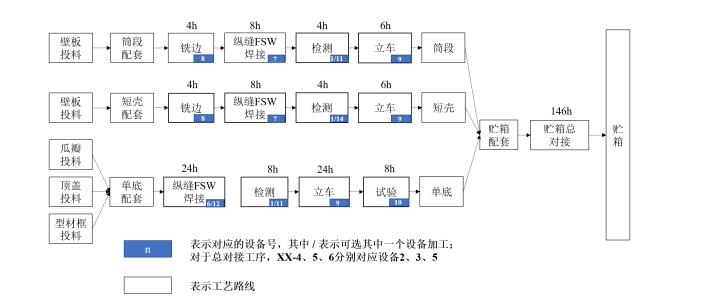 图7 工艺路线图
(3)该车间某年XX-4/5/6贮箱的生产量分别为13、8、5个,产品之间的投产间隔为4天,3种产品所需关键零件种类及个数如表2所示。
表2 产品订单表 产品类型 年任务量/个 关键零件(个/贮箱) 单底 短壳 筒段 XX-4贮箱 13 3 2 1 XX-5贮箱 8 2 2 5 XX-6贮箱 5 4 2 3 合计 26 75 52 68
(4)该车间采用小车的物流运输方式,物流路线如图5中粗线条所示,车间共有2辆物流小车。
(5)每道工序都需要多名工人进行操作,工人行走路线和车辆运行路线基本相同。
(6)该车间设备加工时间存在一定随机性,在仿真模型中设定加工时间服从截尾正态分布。
(7)单底零件经过无损检测工序时,存在一定的返工几率,不合格的单底返回立车工序重新加工。
通过多目标智能优化算法结合仿真进行优化,同时考虑多个优化目标,更符合实际生产过程中的需求,优化过程如下:
(1)创建仿真优化对象的仿真模型。
(2)优化目标:最小化最大完工时间、最小化设备等待时间。
(3)定义算法:NSGA-Ⅱ(带精英策略的非支配排序的遗传算法),与仿真结合的流程与GA算法大致相同,但不同点是基于采用拥挤度和拥挤度比较算子、引入精英策略提出快速非支配排序算法。NSGA-Ⅱ算法流程如图8所示。
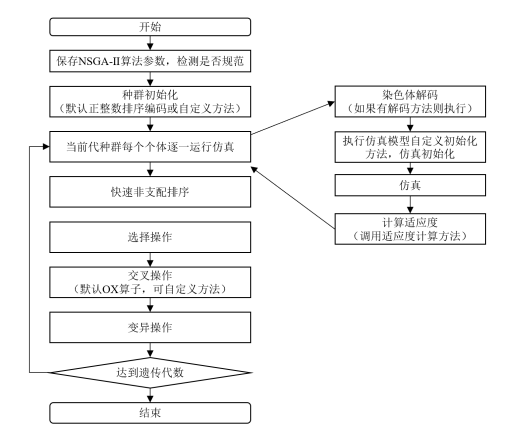 图8 NSGA-Ⅱ算法流程图 (4)定义输入参数以及编码形式:输入参数为26套产品的投产顺序,采用正整数编码的方式对染色体进行编码。 (5)定义仿真模型运行初始化方法(每次试验的每次观察仿真前自动执行并初始化):对染色体进行解码,编码1~13代表XX-4,编码14~21代表XX-5,编码22~26代表XX-6,染色体长度为26。解码后获得新的投产顺序,按投产顺序将产品按照BOM分解为相应的零件,最后输入仿真模型。
(6)定义算法的参数:种群大小设置为50,进化代数设置为20,交叉变异概率分别取0.8和0.1。交叉算子采用部分映射交叉法(PMX)的方式,如图4-10所示,变异算子采用互换变异。
(7)定义适应度计算方法:通过仿真模型运行结果,获取仿真完工时间,并统计每台设备的等待时间,将两个时间值作为适应度返回给算法。
(8)仿真优化自动运行。
(9)优化结果如表3所示,列出了3个非支配解(即Pareto解),可以看出,和优化前结果相比,两个目标值都有大幅降低。
表3 多目标优化非支配解集 序号 完工时间 设备等待时间 染色体编码 优化前 123:5:4:54.865 994:22:15:11.517 [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] 优化后 113:6:0:49.067 864:20:33:55.062 [21,5,1,20,26,23,19,12,11,22,6,8,3,14,2,7,4,25,16,9,18,17,24, 13,15,10] 113:1:49:0 869:22:19:32.720 [26,6,20,8,22,21,1,5,2,19,17,7,15,23,12,4,13,25,18,3,24,11,14,10,9,16] 113:1:6:32.480 869:21:30:7.620 [14,22,8,2,26,18,5,6,19,13,3,23,4,1,24,9,20,16,25,7,11,15,21,10,12,17] (责任编辑:admin) |
