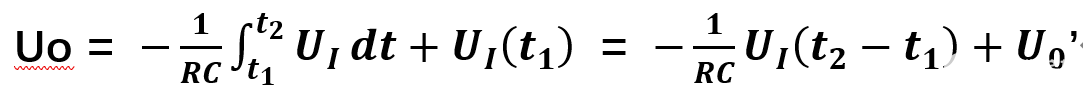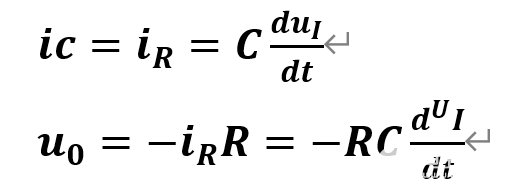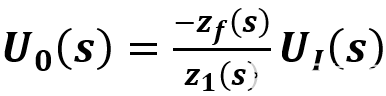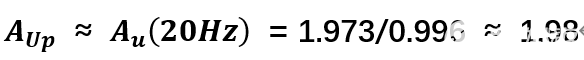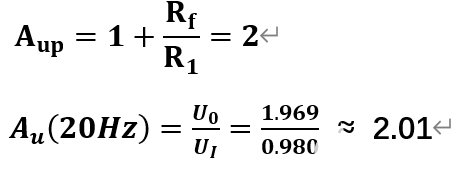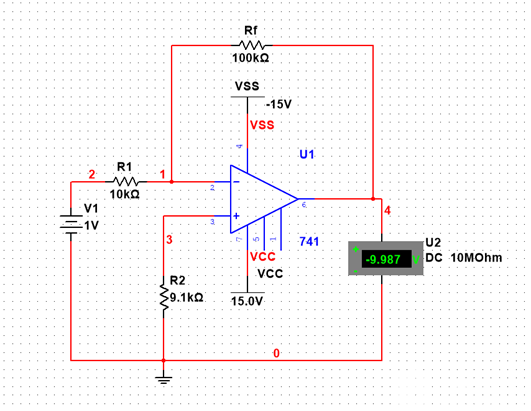
集成运算放大电路线性区运用

集成运放在负反馈情况下工作在线性区，可以构成比例、求和、减法、加减法运算等等多种类型的算术运算电路。下面对单运放构成的反相比例、同相比例和加减法运算电路进行分析，由此导出单运放构成的加减法运算电路输入输出关系的一般计算公式。在此基础上，利用Multisim 软件辅助设计单运放结构的加减法运算电路。

1.基本运算电路

1.1 反相比例运算电路

电路图如图1.1-1所示。

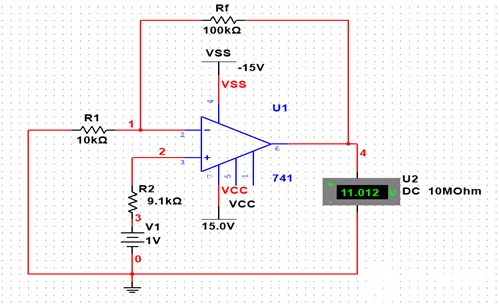
图1.1-1

因为此集成运放电路的对称性，据公式有

Uo = - Rf/R1 * V1 = -10V1 = -10V

与实验结果U2 = -9.987V符合良好。

1.2 同相比例运算电路

电路图如图1.2-1所示。

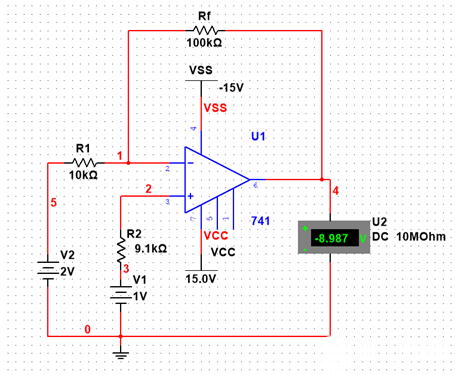
图1.2-1

据公式有Uo = (1 + Rf/R1 )* V1 = 11V1 = 11V

在误差范围内，上式成立。理论结果与实验结果U2 = 11.012V符合良好。

1.3 差分比例运算电路和加减运算电路

差分比例运算电路如图1.3-1所示。

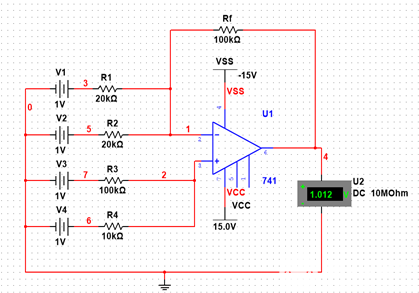
图1.3-1

据公式有Uo = (1 + Rf/R1 )* V1 – Rf/R1*V2 = 11V – 20V = -9V

在误差范围内，上式成立。理论结果与实验结果U2 = -8.987V符合良好。

加减运算电路如图1.3-2所示。

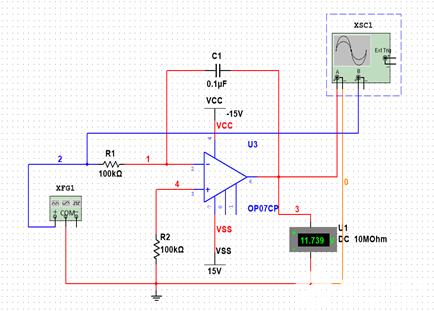
图1.3-2

同理，对于图1.3-2 所示的加减法运算电路，电路的平衡条件是R1//R2//Rf = R3//R4。此时输入输出表达式根据叠加原理，可以看成是由反相端加入的两路输入V1 和V2 所产生的输出量Uo12，与同相端加入的两路输入V3 和V4 所产生的输出量Uo34 共同作用的结果。于是有:

Uo = -Rf/R1* V1 – Rf/R2*V2 + Rf/R3 * V3 + Rf/R4 * V4 = 1V

由此可得由每一路输入信号独立作用时产生的响应，在数值上等于反馈电阻与该路信号的“入端电阻”之比乘以该路信号；若输入信号从运放的反相端加入则极性为负，从同相端加入则极性为正。其实，差分运算电路其实可以算是加减运算电路的特殊情况。

1.4 积分运算电路

电路如图1.4-1所示。

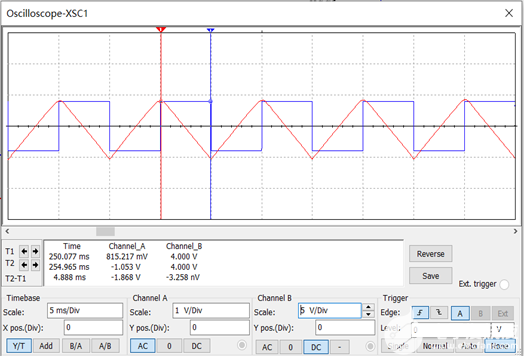
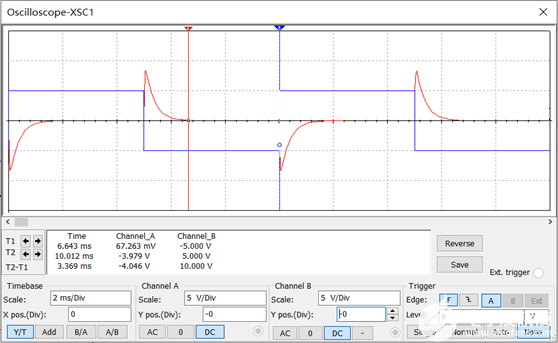
图1.4-1

输入与输出波形如图1.4-2所示。

图1.4-2

对于此积分电路，由于信号源频率为100Hz，则正半个周期（输入电压可看为电压为4V的恒压源）持续时间为5ms，由公式：

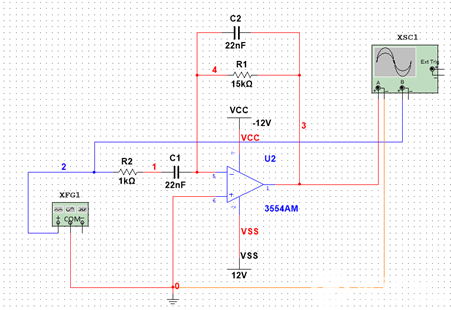
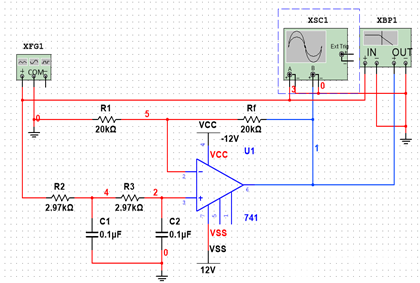
得正半个周期内电压变化幅度ΔUo =-2V（反向增长），与所测结果-1.868V接近。

1.5 微分运算电路

电路如图1.5-1。   

图1.5-1

图1.5-2

微分电路的应用是很广泛的，在线性系统中，除了可作微分的运算外，在数字电路中，常用来作波形变换，例如上例，输入电压为方波时，可以调节电路参数使其输出为尖顶波。

以上我们分析了比例，加减，积分，微分等运算电路。在这些电路中的反馈只是简单的R,C元件。一般来说，他们可以是R,L,C的串联或并联组合。我们可以使用拉普拉斯变换，将Z1和Zf写成相应的Z1(s)，Zf(s),其中s为复频率变量。这样，输出电压为：

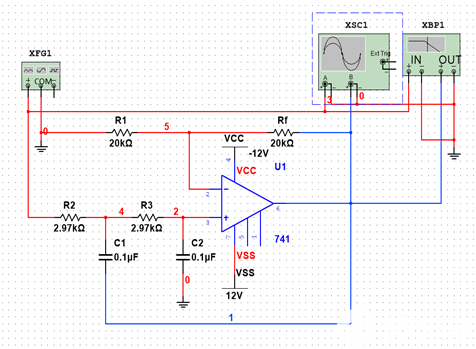
这是反相运算电路的一般表达式。

2.二阶低通/高通、带通/带阻有源滤波电路

滤波电路是一种允许一定频率范围内的信号通过，而对不需要传送的频率范围的信号实现有效抑制的电路。按照频率特性可以将有源滤波电路大致分为四类：低通、高通、带通和带阻滤波器，它们的共同特点是在通带其放大倍数均保持恒定不变，而在阻带放大倍数均为零。而实际滤波电路不可能达到理想滤波特性，只能尽量接近理想滤波特性以满足实际需要。常用的有源滤波电路是二阶压控型滤波电路。这里抽出二阶有源低通滤波电路来分析。

2.1基本型二阶有源低通滤波电路

电路图如图2.1-1所示。

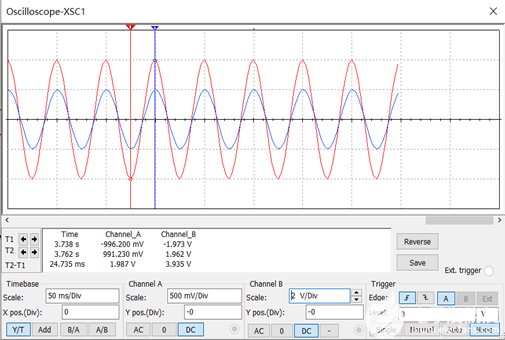
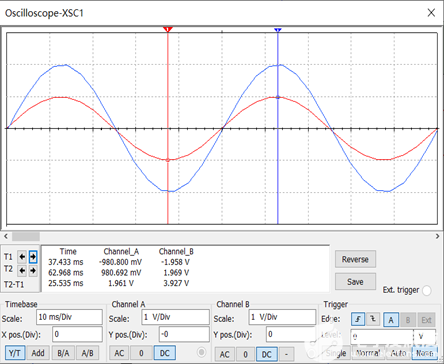
图2.1-1

其中，双击信号源X F G1 图标，设置输入信号Ui 频率为20Hz、峰值为1.0V。示波器数据如图2.1-2所示：

图2.1-2

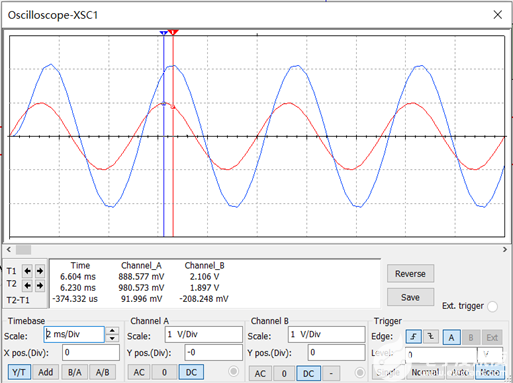
当我们把信号源频率调到200Hz时，有波形数据如图2.1-3所示。

设置输入信号Ui 频率为200Hz、峰值为1.0V，可以看到输入输出波形如图2.1-3所示。从输入和输出波形来看，输出信号的幅度已经明显下降，相位也明显滞后。移动光标T1和T2，Channel A 在T1 处的读数996.686mV ＝ Uip2；Channel B 在T2 处的读数1.403V ＝ Uop2。可得此时的放大倍数为A u = (200H z ) ≈ 1.408 ≈ 1.414，可见，200H z 约为该滤波器的上限截止频率。   

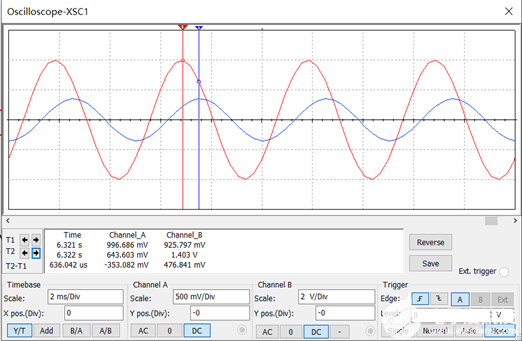
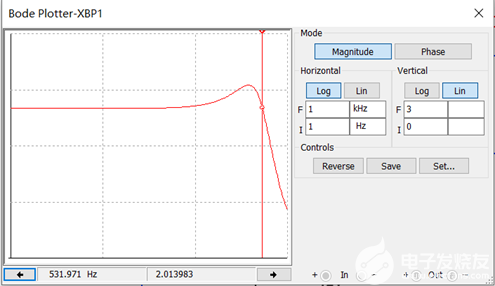
图2.1-3

Bode图数据如图2.1-4所示。

图2.1-4

测得数据如下：

①f1 ＝ 3.995Hz、UO1 ＝ 1.999544V，由于Bode 图仪默认输入信号Ui ＝ 1V，可得通带放大倍数Aup ＝ 1.999544。

②f2 ＝ 199.293Hz、U2 ＝ 1.418673V，此时输出值下降到通带时的70.9%，可知上限截止频率 = 200.0Hz；

③f3 ＝ 401.847Hz、U2 ＝ 827.649mV，此时输出值下降到通带时的41.4%。

测试结果表明，随着输入信号频率的增加，基本型二阶有源低通滤波电路的输出幅度逐渐衰减，在f H 处输出衰减了70.7%，并且阻带衰减速度不够快。

2.2压控型二阶有源低通滤波电路

电路图如图2.2-1所示。

图2.2-1

其中，双击信号源XFG1图标，设置输入信号Ui 频率为20Hz、峰值为1.0V。示波器数据如图2.2-2所示：

图2.2-2

将信号源频率改为f = 200Hz时，得到的输出波形如图2.2-3所示：

图2.2-3

Au（200Hz） ≈ 1.936

可见，在f0 附近引入正反馈以后，输出幅度基本维持不变，改善了f0 附近滤波特性。

Bode图数据如图2.1-4所示。

图2.2-4

测试结果表明，输入信号频率小于f0时，输出基本稳定；在频率大于f0 以后，随着频率增大输出衰减较快。而阻衰减速度远达不到理想，这是二阶滤波电路的固有特性，必须采用高阶滤波才可能解决问题。