|
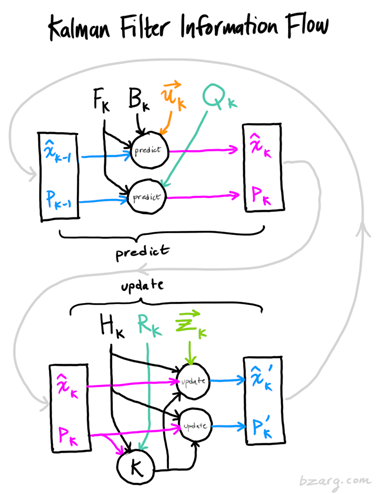
卡尔曼滤波实质上就是基于观测值以及估计值二者的数据对真实值进行估计的过程。预测步骤如图1所示:
图1 卡尔曼滤波原理流程图 假设我们能够得到被测物体的位置和速度的测量值
而此时,
如果我们加入额外的控制量,比如加速度
同时,我们认为我们对系统的估计值并非完全准确,比如运动物体会突然打滑之类的,即存在一个协方差为
由于误差累积的作用,单纯对系统进行估计会导致估计值越来越离谱,因此我们以传感器的观测数据对我们的估计进行修正。我们可以用与预测步骤类似的方法将估计值空间映射至观测值空间,如下式所示:
我们假设观测值为
图2 估计值与观测值概率分布示意图 我们可以认为,这两个概率分布的重叠部分,会更加趋近系统的真实数据,即有更高的置信度,比如我们估计汽车速度是5~10km/h,传感器反馈的速度是8~12km/h,那我们有理由认为汽车的实际速度更趋近于8~10km/h这个区间。 这里将观测值与估计值两个分布的高斯分布相乘,其结果的高斯分布描述如下:
式中: 那么,将估计值
式中, 将式(11)至式(13)中约去
在对单一信号源滤波的场合,由于测量值与估计值具备几乎完全相同的概率分布,为了更好的实现去噪效果,在假定被测对象变化不显著的情况下,可以将之前(1~N)个时间节点的测量值随机作为当前时间节点的测量值,以实现更好的去噪效果。原则上,N取值越大滤波效果越好,但也会导致滤波结果滞后越严重。 2. 算法实现 function output = kalmanFilter(data, Q, R, N) if ~exist('Q', 'var') Q = 0.01;endif ~exist('R', 'var') R = 1;endif ~exist('N', 'var') N = 0;end X = 0;P = 1;A = 1;H = 1; output = zeros(size(data)); for ii = N + 1 : length(data) X_k = A * X; P_k = A * P * A' + Q; Kg = P_k * H' / (H * P_k * H' + R); z_k = data(ii - round(rand() * N)); X = X_k + Kg * (z_k - H * X_k); P = (1 - Kg*H) * P_k; output(ii) = X;end end
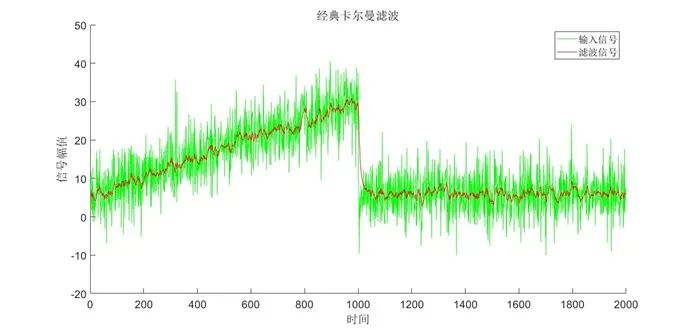
3. 算法分析 采用经典卡尔曼滤波对虚拟信号及真实信号进行滤波,结果如下图所示:
图3 经典卡尔曼滤波对虚拟信号滤波结果
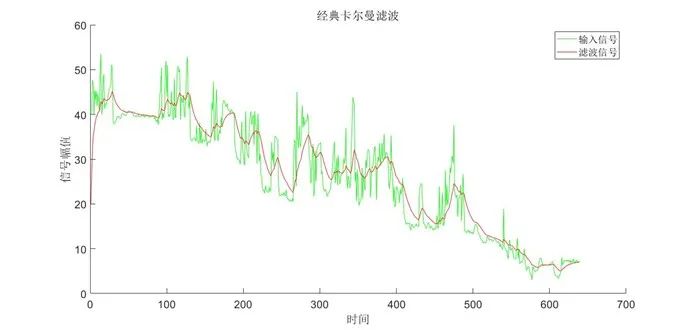
图4 经典卡尔曼滤波对真实信号滤波结果 从滤波结果中可以看出,经典卡尔曼对信号的滤波效果较为优秀,实时性相对较好,计算量需求极小,能够有效去除高斯噪声以及非高斯噪声,基本不受脉冲信号影响。在对被测系统的建模较为精确的条件下,其性能还能够进一步提升。其缺点主要在于需人为给定系统模型,当系统模型不精确时滤波效果会有所下降,但可以通过增加采样频率解决此问题。 建议应用场合:输入信号相对平稳或已知被测系统运动学模型,同时要求运算量极小的场合。 编辑:黄飞 (责任编辑:admin) |

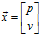 ,在已知上一时刻的最优估计值
,在已知上一时刻的最优估计值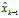 以及它的协方差矩阵
以及它的协方差矩阵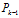 的条件下(初始值可以随意取,但协方差矩阵应为非0矩阵),则有
的条件下(初始值可以随意取,但协方差矩阵应为非0矩阵),则有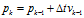 ,
,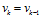 ,即:
,即: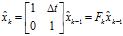 (1)
(1)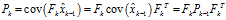 (2)
(2)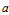 ,此时
,此时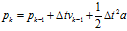 ,
,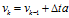 ,则此时:
,则此时: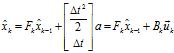 (3)
(3)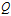 的噪声干扰。因此,我们需要对
的噪声干扰。因此,我们需要对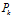 加上系统噪声
加上系统噪声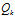 来保证描述的完备性。综上,预测步骤的表达如下所示:
来保证描述的完备性。综上,预测步骤的表达如下所示: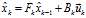 (4)
(4)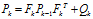 (5)
(5)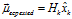 (6)
(6)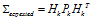 (7)
(7)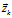 。同时由于观测数据同样会存在噪声干扰问题,比如传感器噪声等,我们将这种噪声的分布用协方差
。同时由于观测数据同样会存在噪声干扰问题,比如传感器噪声等,我们将这种噪声的分布用协方差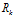 表示。此时,观测值
表示。此时,观测值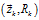 与估计值
与估计值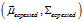 处于相同的状态空间,但具有不同的概率分布,如图2所示:
处于相同的状态空间,但具有不同的概率分布,如图2所示: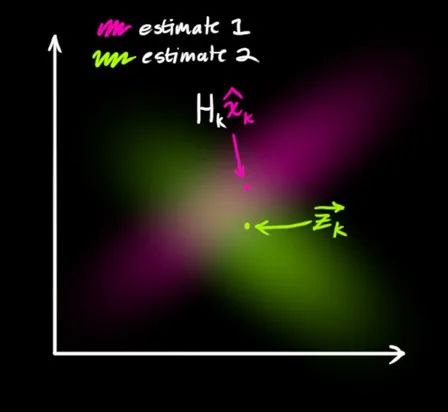
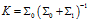 (8)
(8)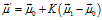 (9)
(9)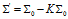 (10)
(10)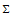 描述高斯分布的协方差,
描述高斯分布的协方差,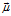 表示高斯分布的均值,矩阵
表示高斯分布的均值,矩阵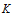 称为卡尔曼增益矩阵。
称为卡尔曼增益矩阵。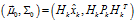 以及观测值
以及观测值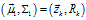 代入式(8)至式(10),可以得到:
代入式(8)至式(10),可以得到: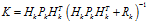 (11)
(11)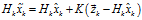 (12)
(12)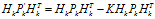 (13)
(13)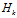 ,并化简可得:
,并化简可得: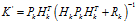 (14)
(14)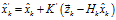 (15)
(15)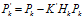 (16)
(16)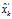 即为我们所得到的最优估计值,同时
即为我们所得到的最优估计值,同时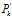 为其对应的协方差矩阵。在实际应用中,只需要使用式(4)、式(5)以及式(14)至式(16)这5个方程即可实现完整的卡尔曼滤波过程。
为其对应的协方差矩阵。在实际应用中,只需要使用式(4)、式(5)以及式(14)至式(16)这5个方程即可实现完整的卡尔曼滤波过程。